L’equilibrio dinamico di un veicolo: determinazione delle reazioni tra suolo e ruote
edutecnica.it
Per studiare l’equilibrio dinamico di un veicolo bisogna innanzitutto fare delle approssimazioni sul tipo di veicolo e su alcune sue caratteristiche.
La nostra analisi porterà all’individuazione delle componenti normali e tangenziali delle reazioni del suolo sulle ruote.
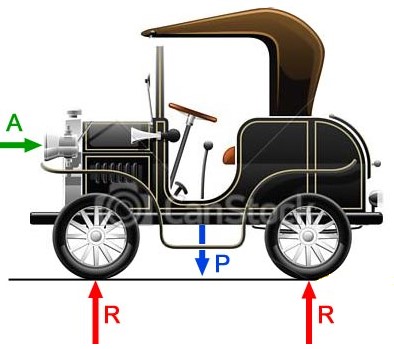
Per semplificare la trattazione considero un veicolo a due assi che sta procedendo su di un percorso inclinato, su di un piano e siano le sue ruote rigide e rotolanti senza strisciare sul suolo:
Nella schematizzazione precedente G rappresenta la posizione del baricentro del veicolo, δ il parametro di attrito volvente; R è il raggio ruota, m la massa del veicolo, α l’angolo d’inclinazione della strada, Fa la reazione dell’aria sul veicolo (composizione vettoriale della resistenza aerodinamica X e della portanza o deportanza Z); v è la velocità del centro ruota rispetto al suolo, w la velocità angolare delle ruote, w. l’accelerazione angolare ed a è l’accelerazione del centro ruota (positiva se concorde con la velocità).
Forze e momenti agenti sul veicolo:
Ruote anteriori:
Le considero assieme; la F1x e la F1y sono rispettivamente la componente orizzontale e verticale della reazione del suolo sulle ruote anteriori.
Per la presenza dell’attrito volvente, tali componenti di reazione, risultano spostate in avanti della quantità δ; ipotizzo stesso δ all’anteriore e al posteriore.
Forze aerodinamiche:
Sposto il vettore Fa in G, e ciò implica l’introduzione del momento di trasporto M.
Forza peso:
La scompongo in due vettori:
Essi sono rispettivamente la componente orizzontale e verticale della forza peso mg.
Azioni inerziali:
Considero la singola ruota:
Tali azioni si oppongono all’accelerazione del corpo rigido.
mo è la massa di una ruota, Ja/R è il momento d’inerzia di ogni singola ruota; se le considero insieme, compare un 2 moltiplicativo.
Considero tutto il veicolo:
Sia Gt il baricentro del telaio del veicolo e considero la risultante delle forze d’inerzia pari ad ma e passante per G.
Così facendo, ottengo questa configurazione:
Sia h l’altezza del baricentro dal suolo, p il passo del veicolo e rispettivamente e e d, il semipasso anteriore e posteriore.
Ho ricavato il punto di partenza per il calcolo dell’equilibrio dinamico del veicolo; il mio obiettivo è quello di determinare le reazioni del suolo sulle ruote.
Calcolo delle reazioni:
Dovendo determinare quattro componenti di reazione, ho bisogno di quattro equazioni di equilibrio; per trovare la prima, considero l’equilibrio alla rotazione, dell’intero veicolo, attorno al punto 2 in figura, ottenendo:
Dall’equilibrio alla rotazione dell’intero veicolo, attorno al punto 1 ottengo che: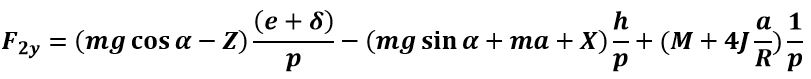
Facendo l’equilibrio alla traslazione orizzontale del veicolo:
Considerando le sole ruote anteriori, ed effettuando l’equilibrio alla rotazione attorno ad O1 (sia Rta la reazione del telaio sulle ruote anteriori):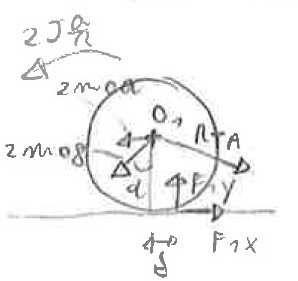
Mettendo a sistema le quattro equazioni precedentemente ricavate:
Si ottengono le quattro incognite (le componenti di reazione tangenziali e normali rispetto al suolo):
Per il corretto utilizzo del precedente sistema di equazioni, devono essere rispettate le seguenti condizioni:
Le ultime due condizioni, sono relative all’aderenza delle ruote sul suolo; non si deve superare il massimo coefficiente di aderenza in direzione longitudinale.
Il sistema di quattro equazioni, con l’aggiunta delle opportune condizioni, risulta perciò fondamentale per determinare alcuni risultati preliminari, come la:
1) Massima accelerazione raggiungibile (al limite di aderenza): essa si ottiene considerando fissati l’angolo d’inclinazione della strada e la velocità del veicolo;
2) Massima pendenza superabile: si ricava ponendo l’accelerazione e velocità all’incirca nulle (con conseguente annullamento delle forze aerodinamiche e del momento M);
3) Massima velocità raggiungibile: si determina fissando l’angolo d’inclinazione e ponendo nulla l’accelerazione del veicolo.
Vi abbiamo mostrato, come, con semplici relazioni di equilibrio ed ipotesi semplificative, si possa a giungere a risultati rilevanti, ai fini del comportamento di un veicolo.