Flap di Gurney con impostazione aerodinamica-matematica

Il flap di Gurney è una soluzione tanto semplice quanto efficiente. Si tratta di una piccola appendice, ossia una paratia aggiunta al bordo di uscita del profilo alare in grado di modificare notevolmente l’aerodinamica del profilo stesso.
L’abbiamo già analizzata dal punto di vista qualitativo insieme all’ala a più elementi; per concentrarci questa volta su un’analisi più quantitativa, dovremo introdurre, almeno parzialmente, la teoria dei profili sottili.

Teoria dei profili sottili

Si tratta di una teoria linearizzata che mira ad ottenere risultati in forma chiusa quantitativamente interessanti dal punto di vista aerodinamico, facendo uso dell’analisi complessa.
Il profilo alare viene descritto mediante due funzioni, una per il dorso e una per il ventre.

Uno degli aspetti fondamentali della teoria è l’imposizione delle giuste condizioni al contorno. Di fatto si tratta della ‘Non penetrazione’ (velocità normale alla superficie nulla), ma dal momento che è una teoria sviluppata per i profili sottili, si suppone che lo spessore del profilo sia almeno un ordine di grandezza inferiore alla lunghezza della corda. In questo modo la condizione al contorno viene imposta sulla corda stessa (y=0) e non più sulla superficie del profilo.

Tenendo conto di una velocità asintotica con incidenza alpha e di una velocità di perturbazione, la condizione di non penetrazione diventa:

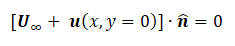
Sviluppando i conti e trascurando gli infinitesimi di ordine superiore, si ottiene un’espressione linearizzata per le condizioni al contorno, ossia un’espressione per la componente verticale della velocità, valida rispettivamente nel caso di descrizione del dorso o del ventre:

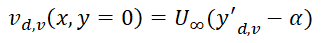
Da cui sommando i risultati per dorso e ventre, e dividendo per due, è possibile ottenere il problema della linea media, fondamentale per capire la successiva trattazione del flap di Gurney:

Dove y’_LM rappresenta l’inclinazione della linea media del profilo rispetto alla direzione orizzontale.

Flap di Gurney e il modello matematico-aerodinamico

Un possibile approccio potrebbe essere quello di leggere con attenzione i risultati che le simulazioni CFD ci offrono. In questo modo, alla luce del comportamento delle linee di corrente e delle zone di alta e bassa pressione, si deducono le conseguenze sulla forza aerodinamica. Alla base di ciò, però, ci deve essere una causa del fenomeno in gioco, la quale ci viene fornita dai risultati notevoli della teoria dei profili sottili.

In particolare, quello su cui ci vogliamo soffermare è il coefficiente di portanza C_L. La determinazione del coefficiente è ottenuta a partire dalla portanza L del teorema di Kutta-Joukowski correttamente adimensionalizzata:

Dove ‘gamma‘ rappresenta la circolazione, ossia la circuitazione del vettore velocità, mentre l è la lunghezza della corda del profilo. Con pagine di integrali e conti (che per vostra fortuna vi risparmio) si arriva ad una formulazione decisamente più semplice, necessaria per trarre delle conclusioni efficaci sul flap di Gurney:

dove:

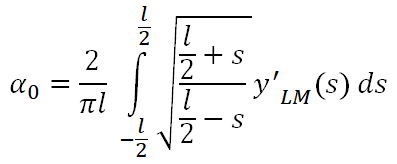
Capiamo il significato dei termini e come sono connessi al flap di Gurney per modificarne l’aerodinamica

Una volta definita l’incidenza della corrente, l’unico termine non costante è alpha₀. All’interno dell’integrale possiamo distinguere due termini: analizziamoli meglio.

Il termine sotto radice quadrata può essere considerata una “funzione peso”. Infatti, immaginando di avere un sistema di riferimento centrato a metà della corda, il profilo si estenderà metà a sinistra, verso il bordo di attacco, e metà a destra, verso il bordo di uscita. Pertanto quando s = – l/2 saremo esattamente nel bordo di attacco, ma la funzione peso si annulla. Viceversa, con s = + l/2, ci troveremo nel bordo di uscita, dove la funzione peso assume valore massimo (tende ad infinito).
Ciò significa che per poter modificare considerevolmente il coefficiente di portanza dovremo primariamente agire sul bordo d’uscita del profilo!

Ora, in ambito automobilistico, quello che ci interessa è ottenere la giusta deportanza. In altri termini bisognerà cercare di aumentare il valore di alpha₀ per far sì che il C_L diventi ancor più negativo. Dunque si aggiunge un flap di Gurney sul bordo di uscita, ossia una paratia a forma di “L” posta verso l’alto. In questo modo andremo ad agire sul secondo termine dell’integrale ( y’_LM ) dato che l’inclinazione della linea media del profilo risulterà ancor più pronunciata.

Cosa succede alla curva di portanza?

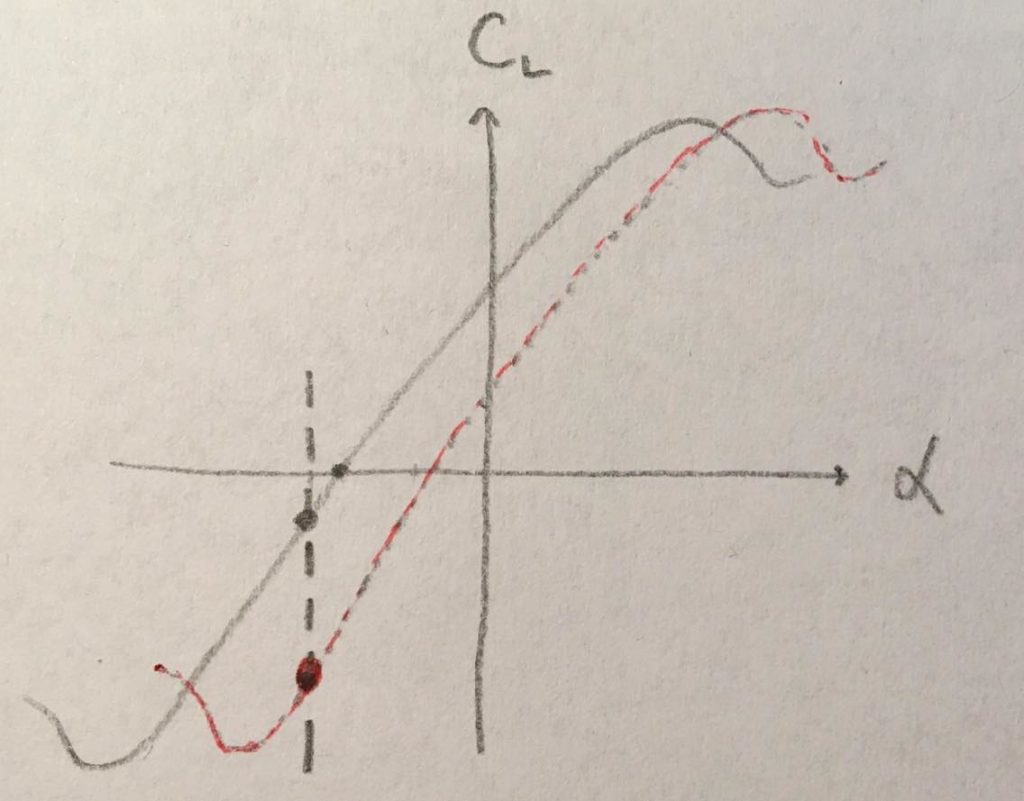
La curva C_L – alpha del profilo si sposterà verso destra. Quindi, avendo cura di mantenere l’incidenza costante, la condizione di utilizzo sarà per un C_L ancor più negativo, ottenendo di fatto una deportanza maggiore.

Attenzione però! Il flap di Gurney deve essere inteso solo come un’ottimizzazione dell’aerodinamica o come una piccola correzione da apportare ad un profilo. Infatti allo stesso modo introduce una buona componente di resistenza non affatto trascurabile e va a modificare l’angolo di progetto del profilo. Si tratta sì di un trucchetto dell’aerodinamica, ma deve essere gestito con cura e soltanto per piccole variazioni.