Il meccanismo di Bourlet: come ottenere la sterzatura cinematica

fastvag.com
Andiamo ad analizzare il meccanismo di sterzo di Bourlet, il quale soddisfa a pieno la condizione di sterzatura cinematica.
 Tale sistema risulta composto da due glifi oscillanti (membri 1 e 3 in figura), asta (membro 2), telaio (membro 4), perni (cerchietti rossi in figura) incernierati all’asta; l’asta è accoppiata prismaticamente (rettangoli verdi in figura) al telaio del veicolo; a è la carreggiata (distanza tra gli assi di kingpin delle ruote).
Tale sistema risulta composto da due glifi oscillanti (membri 1 e 3 in figura), asta (membro 2), telaio (membro 4), perni (cerchietti rossi in figura) incernierati all’asta; l’asta è accoppiata prismaticamente (rettangoli verdi in figura) al telaio del veicolo; a è la carreggiata (distanza tra gli assi di kingpin delle ruote).
Calcolo gradi di libertà:
Per capire come si muove il meccanismo, calcolo i suoi gradi di libertà utilizzando la nota formula di Grübler (nel piano): L ed i indicano rispettivamente i gradi di libertà e le iperstaticità; il primo 3 rappresenta i gradi di libertà posseduti da un corpo rigido nel piano; il secondo 3 è il numero di membri mobili (portamozzi 1 e 2 e asta 3) escluso il telaio; il -2 i gradi di libertà sottratti dalle 3 coppie cinematiche (2 coppie rotoidali tra telaio e aste + 1 coppia prismatica tra asta e telaio); -1 è il numero di gradi di libertà detratti da ognuno dei 2 contatti tra profili coniugati (perni).
L ed i indicano rispettivamente i gradi di libertà e le iperstaticità; il primo 3 rappresenta i gradi di libertà posseduti da un corpo rigido nel piano; il secondo 3 è il numero di membri mobili (portamozzi 1 e 2 e asta 3) escluso il telaio; il -2 i gradi di libertà sottratti dalle 3 coppie cinematiche (2 coppie rotoidali tra telaio e aste + 1 coppia prismatica tra asta e telaio); -1 è il numero di gradi di libertà detratti da ognuno dei 2 contatti tra profili coniugati (perni).
Da tale calcolo, essendo nulle le iperstaticità, deriva un solo grado di libertà del meccanismo nel piano; il grado di libertà consentito è la traslazione dell’asta rispetto al telaio; tale traslazione consente la sterzatura delle ruote.
Quando le ruote non sono sterzate, l’asta traslante, è parallela all’asse delle ruote.
Calcolo condizione di Bourlet:
Immaginando di spostare l’asta verso sinistra (di una quantità x) per sterzare le ruote; alla sinistra del meccanismo si ha che: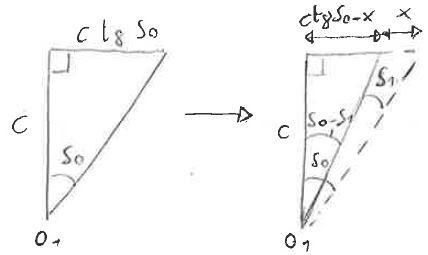 Utilizzando la definizione di tangente di un angolo, si ricava che:
Utilizzando la definizione di tangente di un angolo, si ricava che: A destra invece, succede che:
A destra invece, succede che: Utilizzando ancora la definizione di tangente, si ricava che:
Utilizzando ancora la definizione di tangente, si ricava che: Utilizzando le formule si addizione e sottrazione della tangente:
Utilizzando le formule si addizione e sottrazione della tangente: Si impiega la seguente notazione:
Si impiega la seguente notazione: Si ottiene che:
Si ottiene che: Sommando membro a membro le due quantità precedenti e rielaborando il tutto, ottengo la condizione di Bourlet:
Sommando membro a membro le due quantità precedenti e rielaborando il tutto, ottengo la condizione di Bourlet: Ricordando che la condizione di Ackerman è la seguente:
Ricordando che la condizione di Ackerman è la seguente: Si ottiene che la condizione di Bourlet soddisfa quella di Ackerman quando:
Si ottiene che la condizione di Bourlet soddisfa quella di Ackerman quando: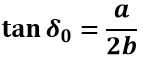
Metodo alternativo per ricavare la condizione di Bourlet:
1) Costruisco un rettangolo di lati a e b;
2) Ribalto tale rettangolo di 180° (verso l’alto) attorno alla linea tratteggiata in figura;
 3) Ottengo la condizione ricavata precedentemente.
3) Ottengo la condizione ricavata precedentemente.
Le problematiche di questo meccanismo di sterzo sono connesse alla difficoltà di mantenere pulita e funzionale la coppia prismatica tra asta traslante e telaio del veicolo. Tale problema si supera utilizzando meccanismi che approssimino la condizione di Ackerman e nei quali si impiegano coppie rotoidali più funzionali delle coppie prismatiche.
Vi abbiamo mostrato come da semplici considerazioni geometriche, si possa ottenere un meccanismo di sterzo che soddisfi la condizione di Ackermann, con notevoli vantaggi in termini di usura delle ruote sul suolo.
